Зміст
- 1 Вивчення явища
- 2 Визначення дисперсії світла, суть явища, пояснення
- 3 Види дисперсії
- 4 Загальна дисперсія
- 5 Міжгрупова дисперсія
- 6 Внутрішньогрупова дисперсія
- 7 Взаємозв’язок
- 8 Властивості дисперсії
- 9 Правило складання дисперсії у статистиці
- 10 Приклад знаходження дисперсії
- 11 Застосування дисперсії світла
- 12 Дисперсія світла: приклади у природі
- 13 Проблеми, що виникають при дисперсії світла
- 14 Відео – що таке дисперсія світла
Вивчення явища
Складний склад сонячного світла виявили Ісаак Ньютон. Він спрямовував із круглого отвору на призму тонкий промінь білого світла, при цьому світло розкладалося на спектр, і на екрані з’являлася лінія з кольорових круглих плям.
Недолік такого способу полягав у тому, що кольорові плями перекривали одна одну і давали чіткий спектр лише з обох боків. Щоб довести, що не сама призма забарвлює світлові промені, Ньютон збирав другою призмою розкладене кольорове проміння, і отримував промінь білого кольору. Коли Ньютон спрямовував на призму монохроматичне світло, розкладання не відбувалося.
Тільки в 1802 році англійський вчений Вільям Волластон вперше використав як джерело променя не круглий отвір, а вузьку щілину, і завдяки цьому отримав безперервний чіткий спектр.
Визначення дисперсії світла, суть явища, пояснення
Визначення 1
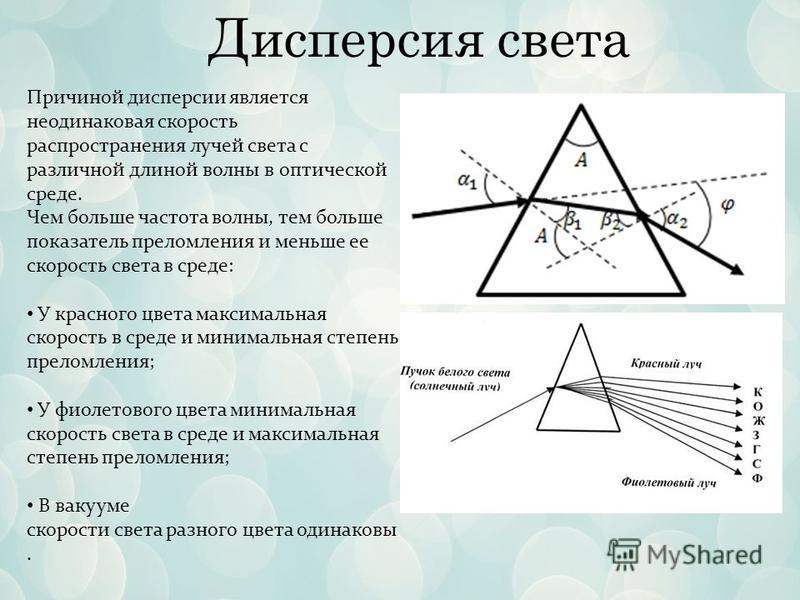
Дисперсія світла – це сукупність явищ, зумовлених залежністю абсолютного показника заломлення частоти коливань (довжини хвилі) світла.
Явище дисперсії виникає у зв’язку з тим, що світлові промені з різною довжиною хвилі мають різну швидкість поширення оптичного середовища.
Формула 1
n=cv,
- де n – відносний показник заломлення,
- с – швидкість світла у вакуумі,
- v — швидкість світла цієї частоти серед.
Так як швидкість поширення хвиль світла в повітрі і вакуумі (має абсолютний показник заломлення, рівний 1) завжди однакова, незалежно від довжини хвилі і, отже, кольору, відносний показник заломлення залежить від швидкості світла в середовищі і назад пропорційний їй.
Зазвичай, що менше довжина світлової хвилі, то більше вписувалося показник заломлення середовища неї і тим менше швидкість поширення хвилі серед:
- у видимому спектрі червоне світло має максимальну фазову швидкість поширення в середовищі та мінімальний ступінь заломлення;
- у фіолетового кольору фазова швидкість поширення серед мінімальна, а ступінь заломлення — максимальна.
Дисперсійний спектр виглядає розтягнутим у короткохвильовій частині. Це з тим, що хвилі різної довжини проходять різний шлях крізь призму. Найбільші відхилення та шлях усередині призми мають промені з високою частотою: відповідно дисперсійний спектр розтягнутий у фіолетовій частині.
За часів І. Ньютона пояснити дисперсію світла не можна було. Для цього було потрібне розуміння природи світлових хвиль, яке тоді тільки починало формуватися. Понад те, навіть електромагнітна теорія Дж. Максвелла не пояснювала причини дисперсії. Ці причини стали зрозумілими надалі, з розвитком уявлення про природу світла в рамках класичної електронної теорії Х. Лоренца.
Стисло можна сказати, що електрони зовнішніх оболонок атомів речовини отримують енергію падаючого випромінювання, під дією якої здійснюють вимушені коливання, і, у свою чергу, також випромінюють. Це вторинне випромінювання поєднується (і інтерферує) з падаючим, і в речовині поширюється результуюча хвиля в тому ж напрямку, як і падаюча. Її швидкість, як випливало з теорії Х. Лоренца, залежить від частоти. А швидкість поширення світла в речовині якраз і визначає коефіцієнт заломлення речовини:
Оскільки швидкість червоних світлових хвиль у речовині виявилася найбільшою, то коефіцієнт заломлення у червоного світла виходить мінімальний. Швидкість фіолетової хвилі найменша, і заломлюється фіолетове світло найсильніше.
Таким чином, коефіцієнт заломлення залежить від частоти випромінювання, а значить, біле світло, що складається з випромінювання різних довжин хвиль, буде переломлюватись різною мірою, залежно від довжини хвилі. У цьому полягає сутність дисперсії.
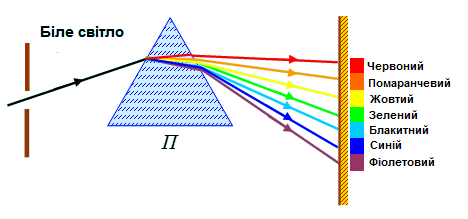
Види дисперсії
Загальна дисперсія вимірює варіацію ознаки у всій сукупності загалом під впливом всіх чинників, що зумовлюють цю варіацію. Вона дорівнює середньому квадрату відхилень окремих значень ознаки від загального середнього значення x і може бути визначена як проста дисперсія або зважена дисперсія.
Внутрішньогрупова дисперсія характеризує випадкову варіацію, тобто. частина варіації, яка обумовлена впливом неврахованих факторів і не залежить від ознаки-фактора, покладеної в основу угруповання. Така дисперсія дорівнює середньому квадрату відхилень окремих значень ознаки всередині групи X від середньої арифметичної групи і може бути обчислена як проста дисперсія або зважена дисперсія.
Таким чином, внутрішньогрупова дисперсія вимірює варіацію ознаки всередині групи та визначається за формулою:
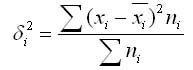
де хі – групова середня;
ni – число одиниць у групі.
Наприклад, внутрішньогрупові дисперсії, які треба визначити в задачі вивчення впливу кваліфікації робітників на рівень продуктивності праці в цеху показують варіації виробітку в кожній групі, викликані всіма можливими факторами (технічний стан обладнання, забезпеченість інструментами та матеріалами, вік робітників, інтенсивність праці тощо) .), крім відмінностей у кваліфікаційному розряді (всередині групи всі робітники мають одну й ту саму кваліфікацію).
Середня всередині групових дисперсій відображає випадкову варіацію, тобто ту частину варіації, яка відбувалася під впливом всіх інших факторів, за винятком фактора угруповання. Вона розраховується за такою формулою:
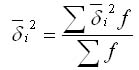
Міжгрупова дисперсія характеризує систематичну варіацію результативної ознаки, яка обумовлена впливом ознаки-фактора, покладеної в основу угруповання. Вона дорівнює середньому квадрату відхилень групових середніх від загальної середньої. Міжгрупова дисперсія розраховується за такою формулою:
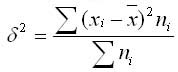
Загальна дисперсія
Як можна помітити, обчислена за наведеним вище визначенням величина характеризує відхилення загалом. Не враховуючи визначальних варіацію чинників. Точніше, з урахуванням усіх, включаючи цілком випадкові. Тому і називається “загальною” і розраховується за формулами, вказаними нижче.
Проста дисперсія, без поділу на групи:
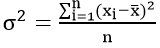
Або в дещо перетвореному вигляді:
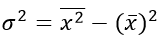
Зважена дисперсія для варіаційного ряду:
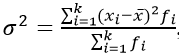
- де xi – значення з ряду;
- fi – частота, кількість повторень;
- k – груп;
- n – кількість варіантів.
Характеристика зверху вказує на середню величину.
Міжгрупова дисперсія
Характеризує систематичне відхилення, що виникає через чинник, яким вироблялося виділення ознак групи. Тому також називається “факторною”.
Як знайти цю дисперсію? За формулою:
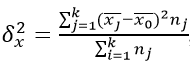
- де k – кількість груп;
- nj – елементів у групі з індексом j.
Внутрішньогрупова дисперсія
Виникає через хаотичну причину, не пов’язану з причиною зробленої вибірки. Неврахований фактор. Ще позначається як «залишкова».
Наприклад, розглядається кількість випущених деталей за місяць кожним фрезерувальником цеху.
Як критерій відбору в групу вибираємо вік обладнання. Він і не впливатиме на продуктивність усередині добірки: там верстати у всіх практично однакові.
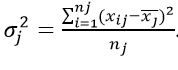
Якщо обчислити середню величину від усіх групових,
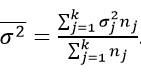
то отримаємо характеристику випадкового розкиду. Іншими словами, складова варіації, яка залежить від чого завгодно, крім фактора відбору.
Взаємозв’язок
Відповідно до правила додавання, загальна D[X] включає середні вирази залишкової та факторної. І це логічно, оскільки враховує і випадкову зміну у групі, і систематичну у факторній.
Властивості дисперсії
1. Якщо всі значення ознаки зменшити (збільшити) на ту саму постійну величину, то дисперсія від цього не зміниться.
2. Якщо всі значення ознаки зменшити (збільшити) в те саме число разів n, то дисперсія відповідно зменшиться (збільшити) в n^2 разів.
Правило складання дисперсії у статистиці
Відповідно до правила складання дисперсій загальна дисперсія дорівнює сумі середньої з внутрішньогрупових та міжгрупових дисперсій:
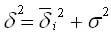
Сенс цього правила полягає в тому, що загальна дисперсія, яка виникає під впливом всіх факторів, дорівнює сумі дисперсій, що виникають під впливом всіх інших факторів, та дисперсії, що виникає за рахунок фактора угруповання.
Користуючись формулою складання дисперсій, можна визначити за двома відомими дисперсіями третю невідому, а також судити про силу впливу групувальної ознаки.
Приклад знаходження дисперсії
На цій сторінці описано стандартний приклад знаходження дисперсії, також Ви можете переглянути інші завдання на її знаходження
Приклад 1. Є такі дані щодо групи з 20 студентів заочного відділення. Потрібно побудувати інтервальний ряд розподілу ознаки, розрахувати середнє значення ознаки та вивчити його дисперсію
| № пп | Рост, см |
| 1 | 159 |
| 2 | 160 |
| 3 | 161 |
| 4 | 162 |
| 5 | 162 |
| 6 | 164 |
| 7 | 166 |
| 8 | 169 |
| 9 | 170 |
| 10 | 170 |
| 11 | 171 |
| 12 | 171 |
| 13 | 172 |
| 14 | 174 |
| 15 | 176 |
| 16 | 176 |
| 17 | 178 |
| 18 | 181 |
| 19 | 183 |
| 20 | 192 |
Побудуємо інтервальне угруповання. Визначимо розмах інтервалу за формулою:
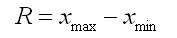
- де X max – максимальне значення групувального ознаки;
- X min-мінімальне значення групувальної ознаки;
- n – кількість інтервалів:
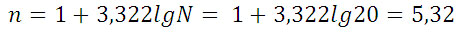
Приймаємо n=5. Крок дорівнює: h = (192 – 159) / 5 = 6,6
Складемо інтервальне угруповання
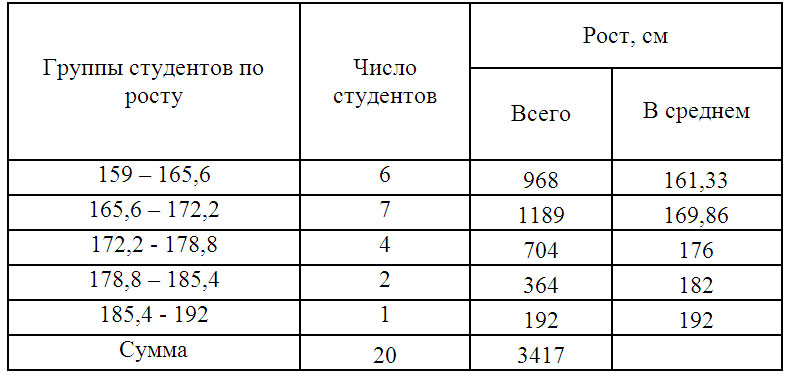
Для подальших розрахунків збудуємо допоміжну таблицю:
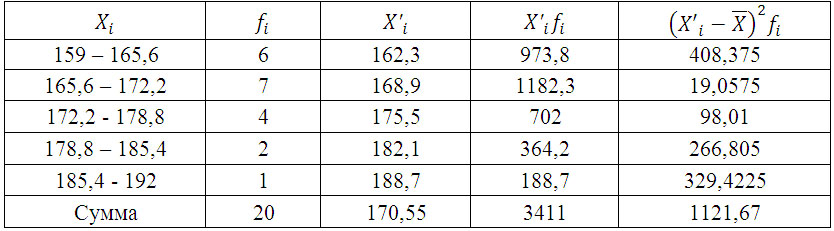
X’i – середина інтервалу. (наприклад, середина інтервалу 159 – 165,6 = 162,3)
Середню величину зростання студентів визначимо за формулою середньої арифметичної зваженої:
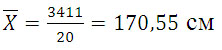
Визначимо дисперсію за такою формулою:
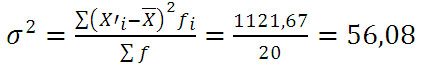
Формулу дисперсії можна перетворити так:
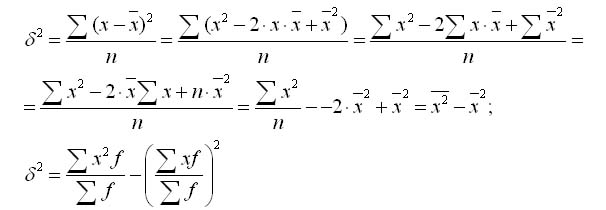
З цієї формули випливає, що дисперсія дорівнює різниці середньої квадратів варіантів і квадрата і середньої.
Дисперсія в варіаційних рядах з рівними інтервалами способу моментів може бути розрахована наступним способом при використанні другої властивості дисперсії (розділивши всі варіанти на величину інтервалу). Визначення дисперсії, обчисленої за способом моментів, за такою формулою менш трудомісткий:
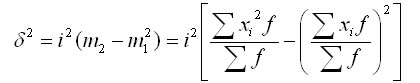
де i – Величина інтервалу;
А – умовний нуль, в якості якого зручно використовувати середину інтервалу, що має найбільшу частоту;
m1 – квадрат моменту першого порядку;
m2 – момент другого порядку
Дисперсія альтернативної ознаки (якщо в статистичній сукупності ознака змінюється так, що є тільки два варіанти, що взаємно виключають один одного, то така мінливість називається альтернативною) може бути обчислена за формулою:
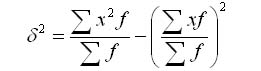
Підставляючи до цієї формули дисперсії q =1- р, отримуємо:
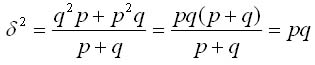
Застосування дисперсії світла
Дисперсія в огранованому діаманті, яку демонструє картинка нижче.

На явище дисперсії засноване застосування рідких кристалів, що мають властивості як рідин (плинність), так і кристалів (анізотропія). Проходячи через рідкий кристал, світло розпадається на два промені: зазвичай поширюється і заломлений. З їх допомогою виявляють пари шкідливих хімічних сполук, гамма- та ультрафіолетові випромінювання.
Застосовують в інформаційній техніці (рідкокристалічні індикатори та екрани), медицині, мікросхемах, на виробництві. Наприклад, рідкі кристали застосовуються у виробництві «розумного скла», здатного змінювати опалесценцію та коефіцієнти світлопропускання та поглинання тепла.
У «кільці настрою» під шаром скла або пластику знаходяться рідкі кристали, тому воно змінює колір залежно від температури.
Дисперсія світла: приклади у природі
- Веселка – це результат відображення та дисперсії світла в крапельках води. Саме дисперсія відповідальна за те, що веселка має вигляд спектру, а не білої дуги. Так як крапельки води можуть відрізнятися тільки розмірами, то розташування веселки завжди приблизно однаково. Центр кола, яке описує веселка, завжди лежить на прямій, що проходить через Сонце та око спостерігача, тобто одночасно бачити сонце та веселку без використання дзеркал неможливо.
- Дисперсія світла в широких кристалах льоду є основою такого атмосферного оптичного явища, як гало. Крижані кристали можуть бути різного розміру, форми та по-різному орієнтовані в повітрі, тому гало буває дуже різноманітним. Існує близько сотні різних видів гало.
- Світлові стовпи, несправжні сонця (паргелії) за деякими класифікаціями також відносяться до гало. Їхній вигляд обумовлений дисперсією світла в крижаних кристалах.
- “Привид Броккена”. Явище, що отримало назву «броккенський привид», є тінь спостерігача, що падає на нижче хмару, і зазвичай спостерігається в горах.
Проблеми, що виникають при дисперсії світла
Дисперсія світла – гарне і ефектне явище, але воно також може завдавати неприємностей. Перші спостереження над небом проводилися з допомогою телескопів, які мали одинарні скляні лінзи.
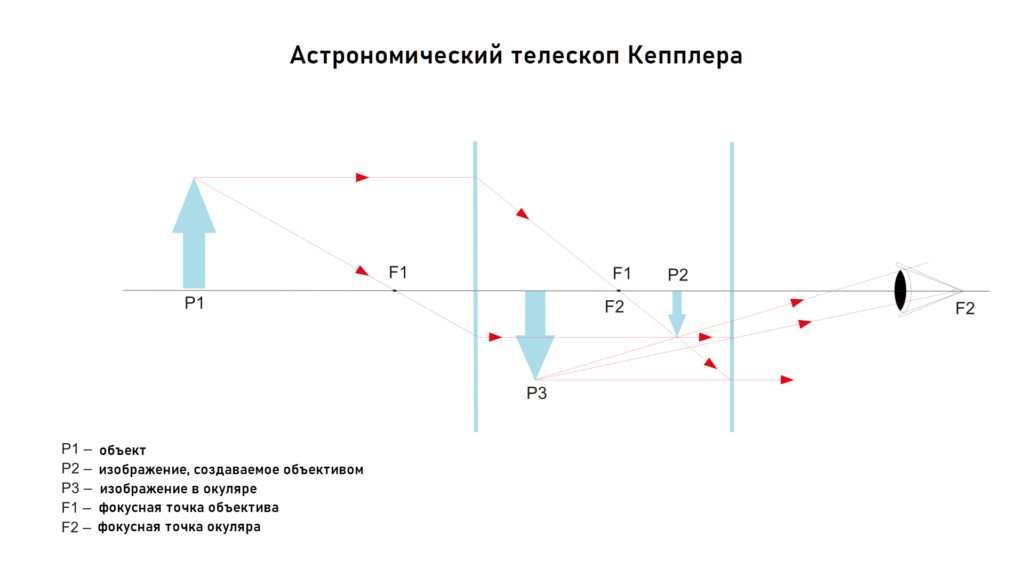
Мал. 4. Заломлення світла у лінзах астрономічного телескопа
Коли промінь світла проходить через лінзу і заломлюється, як у призмі, особливо в «товстих» лінзах, світло може розщеплюватися на основні кольори. Кожен колір має свою фокусну точку (фокус) – тому немає єдиної точки, в якій сходяться всі світлові промені. В результаті ви можете помітити колірну облямівку (див. малюнок 4) навколо об’єктів, що спостерігаються, і відчути зниження гостроти зору.
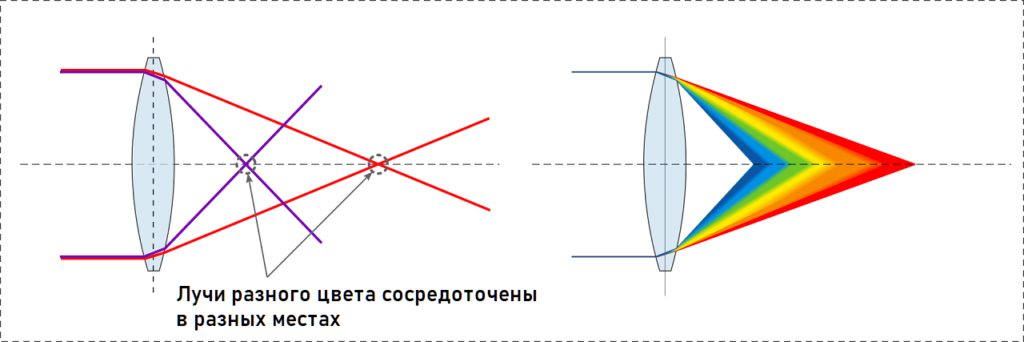
Мал. 5. Хроматична аберація (кольорова облямівка)
Це називається хроматичної аберацією. Визначення цього поняття таке:
Хроматична аберація – це дефект лінзи, викликаний розкладанням білого світла на складові кольору, так що кожен колір має власний фокус, розташований на різній відстані від лінзи.
Хроматична аберація впливає на якість зображення як при астрономічних спостереженнях, які проводяться за допомогою простих телескопів, так і в процесі звичайної зйомки, оскільки фотоапарати оснащені пластиковими або скляними лінзами. Цей ефект можна усунути, використовуючи замість окремих лінз систему відповідним чином підібраних лінз (ахроматична система).