Зміст
Що таке трикутник
Трикутник – це геометрична фігура, утворена з’єднанням відрізками трьох, що не лежать на одній прямій точок.
Ці точки називаються вершинами трикутника. Відрізки, що з’єднують ці точки, називаються сторонами трикутника.
Як позначається трикутник
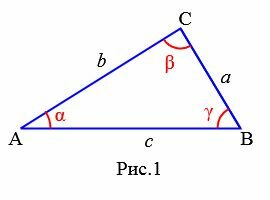
Трикутник позначається знаком ⊿. Наприклад, трикутник ABC позначається так: ⊿ABC. Цей трикутник можна позначати так: ⊿BAC, ⊿CBA і т.д.
Кути трикутника позначають так ∠ BAC , ∠ ABC , ∠ BCA . Ці ж кути коротко позначають також ∠A , ∠B , ∠C , відповідно. Кути трикутника прийнято позначати також грецькими літерами α, β, γ і т.д. Сторони трикутника позначають так AB , BC , AC . Прийнято також сторони позначати однією малою літерою, причому сторона навпроти кута A , позначається буквою a , сторона навпроти кута B − b , сторона навпроти кута C − c. Сума трьох сторін трикутника називається периметром трикутника.
Як відомо, два трикутники називаються рівними, якщо при накладенні один на одного їх можна поєднати. На Рис.2 представлені два трикутники ABC і A1B1C1 . _ Трикутник ABC можна накласти на трикутник A 1 B 1 C 1 так, щоб вершини та сторони цих трикутників попарно поєдналися. Очевидно, що при цьому поєднаються і відповідні кути.
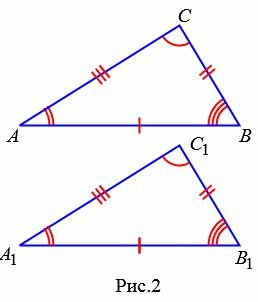
Вищевикладене можна сформулювати так:
Якщо два трикутники рівні, то елементи (сторони та кути) одного трикутника відповідно дорівнюють елементам іншого трикутника. Рівність трикутників ABC і A 1 B 1 C 1 позначається так:
Перша ознака рівності трикутників
Теорема 1. Якщо дві сторони та кут між ними одного трикутника відповідно дорівнюють двом сторонам і куту між ними іншого трикутника, то ці трикутники рівні.
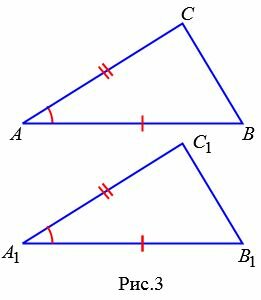
Доведення. Розглянемо трикутники ABC та A 1 B 1 C 1 (Рис.3). Нехай AB = A 1 B 1 , AС = A 1 С 1 і A = ∠ A 1 . Доведемо, що .
Так як ∠ A = ∠ A 1 , то трикутник ABC можна накласти на трикутник A 1 B 1 C 1 так, щоб вершини A і A 1 збігалися, а сторони AB і AС наклалися на промені A 1 B 1 і A 1 C 1 , відповідно.
Так як за умовою теореми AB = A 1 B 1 , AС = A 1 С 1 , то сторона AB суміситься зі стороною A 1 B 1 , а сторона AС − зі стороною A 1 С 1. Тоді суміщаться B і B 1 , C і З 1 . Отже сторона BC поєднається зі стороною B 1 C 1 . Тобто трикутники ABCта A 1 B 1 C 1 повністю сумісні. Теорему доведено.
Друга ознака рівності трикутників
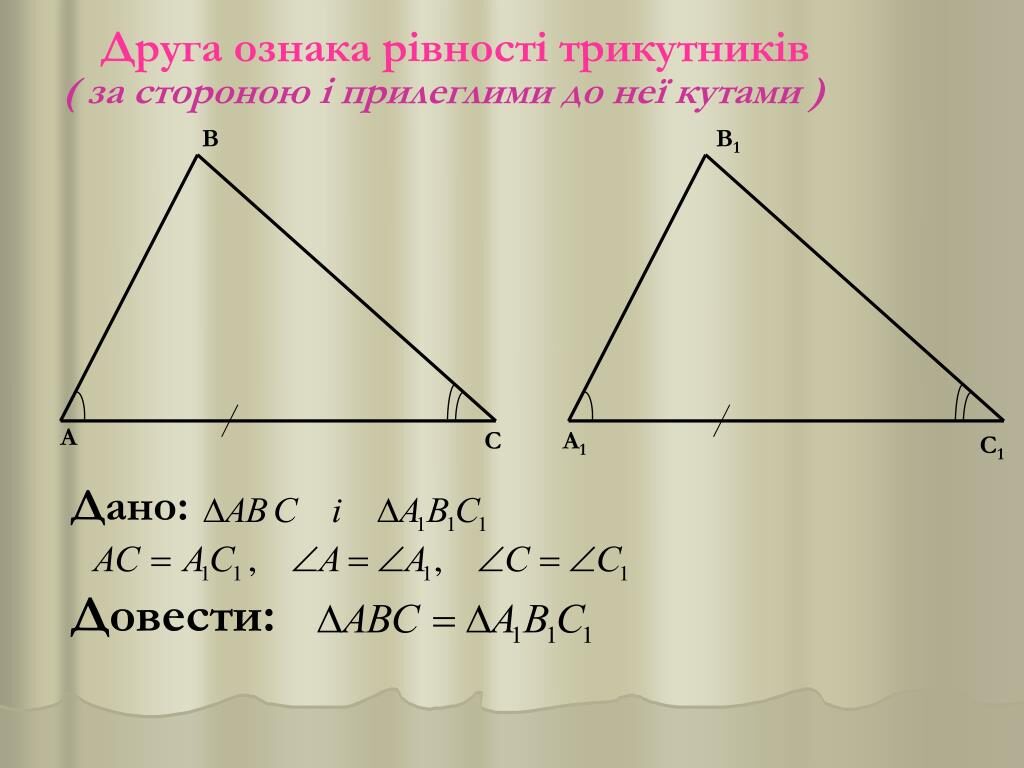
Теорема 2. Якщо сторона і два кути одного трикутника, що до неї прилягають, відповідно рівні стороні і двом прилеглим до неї кутам іншого трикутника, то ці трикутники рівні.
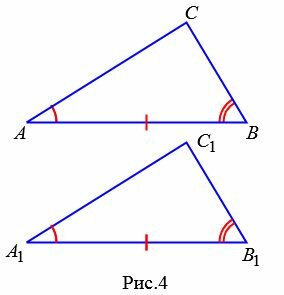
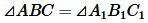
Доведення. Розглянемо трикутники ABC і A1B1С1 ( Рис.4 ) . _ Нехай AB = A 1 B 1 , ∠ A = ∠ A 1 , ∠ B = ∠ B 1 . Доведемо, що .
Накладемо трикутник ABC на трикутник A 1 B 1 С 1 так, щоб вершина A поєднувалася з вершиною A 1 , сторона AB − зі стороною A 1 B 1 (за умовою теореми AB = A 1 B 1 ), а вершини C та С 1 виявилися по одну сторону від прямої A 1 B 1 .
Так як ∠ A = ∠ A 1 і ∠ B = ∠ B 1 , то сторона AС накладеться на промінь A 1 C 1 а сторона BС − на промінь B 1 С 1 . Тоді вершина C опиниться на промені A 1 C 1 і на промені B 1 C 1 . Тобто. вона опиниться на перетині цих променів і, отже, вершина C поєднається із загальною точкою променів A 1 C 1 і B 1З 1 , тобто. з вершиною C1 . Таким чином сумісні сторони AC і A 1 C 1 BC і B 1 C 1 . Тобто трикутники ABC та A 1 B 1 С 1 повністю суміщаються, тому вони рівні. Теорему доведено.
Третя ознака рівності трикутників
Теорема 3. Якщо три сторони одного трикутника відповідно дорівнюють трьом сторонам іншого трикутника, то ці трикутники рівні.
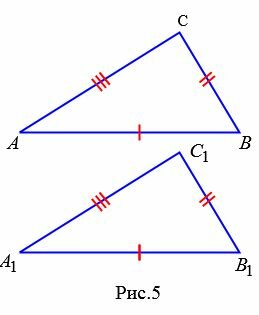
Доведення. Розглянемо трикутники ABC і A1B1С1 . _ _ _ _ Нехай AB = A 1 B 1 , AC = A 1 C 1 та BC = B 1 C 1 . Доведемо, що . Докладемо трикутник ABC до трикутника A 1 B 1 З 1 так, щоб вершина A поєднувалася з вершиною A 1 вершина B
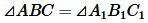
поєднувалася з вершиною B 1 , а вершини З і С 1 знаходилися по різні боки від прямої A 1 B 1 .
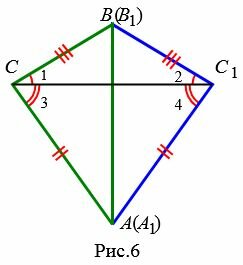
Можливі три варіанти: промінь CC 1 проходить усередині кута ACB (Рис.6); промінь CC 1 збігається з однією зі сторін кута ACB (Мал.7); промінь CC 1 проходить поза кутом ACB (Рис.8). Розглянемо ці три випадки окремо.
Варіант 1 (Рис.6). Так як за умовою теореми AC = A 1 C 1 і BC = B 1 C 1 то трикутники A СС 1 і B СС 1 рівнобедрені. Тоді ∠1=∠2 і ∠3=∠4 і, отже:
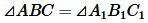
Маємо AC = A 1 C 1 , BC = B 1 C 1 ∠ ACB = ∠ A 1 C 1 B 1 і за першою ознакою рівності трикутників . Теорему доведено.
Варіант 2 (Мал.7). Так як за умовою теореми AC = A 1 C 1 і BC = B 1 C 1 то трикутник B СС 1 рівнобедрений. Тоді ∠1=∠2. Маємо: AC = A 1 C 1 , BC = B 1 C 1 , ∠1=∠2 і за першою ознакою рівності трикутників
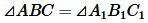
. Теорему доведено.
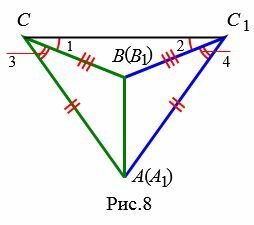
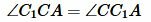
Варіант 3 (Рис.8). Так як за умовою теореми AC = A 1 C 1 і BC = B 1 C 1 то трикутники A СС 1 і B СС 1 рівнобедрені. Тоді ∠1=∠2 і , отже:
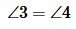
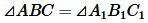
Маємо AC = A 1 C 1 , BC = B 1 C 1 і за першою ознакою рівності трикутників . Теорему доведено.
Завдання та рішення
Завдання 1. На сторонах кута CAD відзначені точки B і E так, що точка B лежить на відрізку AC , а точка E – на відрізку AD , причому AC=AD та AB=AE . Доведіть, що ∠ CBD = ∠ DEC (Рис.9).
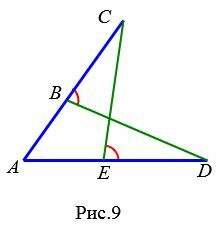
Доведення. AC = AD , AE = AB , ∠ CAD загальний для трикутників CAE та DAB . Тоді за першою ознакою рівності трикутників (теорема 1) ⊿ ACE =⊿ ADB . Отже ∠ DBA = ∠ AEC . Оскільки кути CBD та DBA суміжні, то CBD =180°−∠ DBA . Аналогічно CED = 180 ° – AEC . Тобто ∠ CBD = ∠ DEC . Кінець доказу .
Завдання 2. За даними малюнка рис.10 доведіть, що OP=OT , ∠ P =∠ T
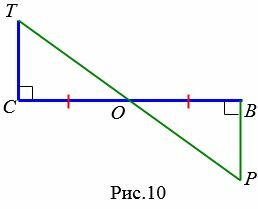
Доведення. OC = OB , ∠ TCO = ∠ PBO = 90 °. Кути TOC і POB вертикальні (отже рівні) тоді, вторинною ознакою рівності трикутників (теорема 2), ⊿ TCO =⊿ PBO . Кінець доказу .
Завдання на ознаку рівності трикутників: друга та третя ознака
Друга ознака рівності трикутників
Якщо сторона трикутника і два кути, що прилягають до неї, рівні стороні іншого трикутника і двом прилеглим кутам, то ці два трикутники рівні.
Звідси випливає така теорема:
Якщо сторона трикутника і два до неї кути дорівнюють стороні іншого трикутника і двом кутам, то ці два трикутники рівні.
Третя ознака рівності трикутників
Якщо три сторони трикутника дорівнюють трьом сторонам іншого трикутника, то такі трикутники рівні.
Завдання
Завдання 1
Дано:
ABC – рівнобедрений трикутник.
АМ і BN бісектриси кута.
Довести: AM = BN.
Доказ:
Трикутники AMB і BNA – рівні (за другою ознакою – кут-сторона-кут) тому що:
1. ∠CAB = ∠CBA
2. AB – в обох трикутниках. 3. ∠MAB
= ∠NBA = 1/2 ∠CAB .
Відрізки AM та BN є відповідними у цих рівних трикутниках, і, отже, AM = BN.
Завдання 2
Дано:
ABC – трикутник,
CM – медіана,
AA 1 ⊥ CM та BB 1 ⊥ CM.
Довести: АА 1 = ВР 1 .
Доказ:
1. ∠BB 1 M = ∠AA 1 M = 90°,
2. ∠AMA 1 = ∠BMB 1 як вертикальні,
3. AM = BM.
Отже ΔAA 1 M = ΔBB 1 M (за другою ознакою).
Тоді AA 1 = BB 1 як відповідні сторони цих трикутниках.
Завдання 3
Доведіть, що перпендикуляри, проведені з будь-якої точки бісектриси кута щодо його сторін, вирізають на них рівні відрізки.
Доказ:
Давайте припустимо, що ∠AOB точка M – невизначена точка на бісектрисі OL. (fig.40)
Візьмемо, що MP OA і MQ OB. Для того, щоб довести, що OP = OQ, достатньо довести що OPM = OQM.
Але ΔOPM = ΔOQM(за другою ознакою), тому що
1. OM – загальна сторона,
2. ∠QOM = ∠POM (OL є бісектриса),
3. ∠OQM = ∠OPM = 90°, звідки OP = OQ
Завдання 4
Доведіть, що якщо у трикутнику висота та бісектриса, проведені з однієї вершини, рівні, то трикутник рівнобедрений.
Доказ:
Позначимо, що ΔABC висота та бісектриса, проведені з вершини C, збігаються (рис. 41).
А, щоб довести, що AC = BC, тобто. ABC є рівнобедреним, достатньо довести, що APC = BPC.
Але ΔAPC = ΔBPC (за другою ознакою) тому що
1. ∠ACP = ∠BCP (CP – бісектриса)
2. ∠ACP = ∠CPB = 90° (CP – висота)
3. CP – загальна сторона
Відтак AC = BC ⇒ ABC – рівнобедрений
Завдання 5
Дано:
AB = A 1 B 1
BC = B 1 C 1
AM = A 1 M 1 – медіани
Доведіть ΔABC = ΔA 1 B 1 C 1
Доказ:
Давайте подивимося на трикутники ΔABM та ΔA 1 B 1 M 1 .
1. AB = A 1 B 1
2. AM = A 1 M 1
3. BM =1221BC
B 1 M 1 =1221B 1 C 1
Але BC = B 1 C 1 отже
BM = B 1 M 1
⇒ ΔABM = ΔA 1 B 1 M 1 (за третьою ознакою).
Отже, ∠ABC = ∠A 1 B 1 C 1
Давайте подивимося на трикутники ΔABC і ΔA 1 B 1 C 1
1. AB = A 1 B 1
2. BC = B 1 C 1
3. ABC = A 1 B 1 C 1
Тоді, ΔABC = ΔA 1 B 1 C 1 – рівні за першою ознакою.